Relational Algebra in DBMS: Operators, Examples & SQL Equivalents

What is Relational Algebra in DBMS?

Relational Algebra came in 1970 and was given by Edgar F. Codd (Father of DBMS). It is also known as Procedural Query Language(PQL) as in PQL, a programmer/user has to mention two things, "What to Do" and "How to Do".

Suppose our data is stored in a database, then relational algebra is used to access the data from the database.

The First thing is we have to access the data, this needs to be specified in the query as "What to Do", but we have to also specify the method/procedure in the query that is "How to Do" or how to access the data from the database.

Stop learning AI in fragments—master a structured AI Engineering Course with hands-on GenAI systems with IIT Roorkee CEC Certification

Types of Relational Operations in DBMS

In Relational Algebra, we have two types of Operations.

• Basic Operations
• Derived Operations

Applying these operations over relations/tables will give us new relations as output.

Basic Operations

Six fundamental operations are mentioned below. The majority of data retrieval operations are carried out by these. Let's know them one by one.

But, before moving into detail, let's have two tables or we can say relations STUDENT(ROLL, NAME, AGE) and EMPLOYEE(EMPLOYEE_NO, NAME, AGE) which will be used in the below examples.

STUDENT

EMPLOYEE

Select (σ)

Select operation is done by Selection Operator which is represented by "sigma"(σ). It is used to retrieve tuples(rows) from the table where the given condition is satisfied. It is a unary operator means it requires only one operand.
Notation : σ p(R)
Where σ is used to represent SELECTION
R is used to represent RELATION
p is the logic formula
Let's understand this with an example:
Suppose we want the row(s) from STUDENT Relation where "AGE" is 20

This will return the following output:

Build an AI-First Career, Master the Complete Skillset

Choose from our industry-leading programs designed for career success

NSDC Certified

Modern Software and AI Engineering Program

Master full-stack development with AI integration

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

Modern Data Science and ML with specialisation in AI

Advanced data science techniques with AI specialization

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

Advanced AIML with Specialisation in Agentic AI

Deep dive into AIML with focus on Agentic systems

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

DevOps, Cloud & AI Platform Engineering

Build and manage AI-powered cloud infrastructure

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

NSDC Certified

AI Engineering Advanced Certification by IIT-Roorkee

Premier AI engineering certification from IIT-Roorkee

3 MonthsDuration

AI-LedCurriculum

Career SupportSupport

Go to Program

NSDC Certified

AI Forward Deployed Engineer Program

Full-stack engineering, production AI and client-facing consulting

12 MonthsDuration

AI-LedCurriculum

Career SupportSupport

+1000 more

Go to Program

Project (∏)

Project operation is done by Projection Operator which is represented by "pi"(∏). It is used to retrieve certain attributes(columns) from the table. It is also known as vertical partitioning as it separates the table vertically. It is also a unary operator.
Notation : ∏ a(r)
Where ∏ is used to represent PROJECTION
r is used to represent RELATION
a is the attribute list
Let's understand this with an example:
Suppose we want the names of all students from STUDENT Relation.

This will return the following output:

As you can see from the above output it eliminates duplicates.
For multiple attributes, we can separate them using a ",".

Above code will return two columns, ROLL and NAME.

Union (∪)

Union operation is done by Union Operator which is represented by "union"(∪). It is the same as the union operator from set theory, i.e., it selects all tuples from both relations but with the exception that for the union of two relations/tables both relations must have the same set of Attributes. It is a binary operator as it requires two operands.
Notation: R ∪ S
Where R is the first relation
S is the second relation

If relations don't have the same set of attributes, then the union of such relations will result in NULL.

Let's have an example to clarify the concept:
Suppose we want all the names from STUDENT and EMPLOYEE relation.

As we can see from the above output it also eliminates duplicates.

Set Difference (-)

Set Difference as its name indicates is the difference between two relations (R-S). It is denoted by a "Hyphen"(-) and it returns all the tuples(rows) which are in relation R but not in relation S. It is also a binary operator.
Notation : R - S
Where R is the first relation
S is the second relation

Just like union, the set difference also comes with the exception of the same set of attributes in both relations.

Let's take an example where we would like to know the names of students who are in STUDENT Relation but not in EMPLOYEE Relation.

This will give us the following output:

Cartesian product (X)

Cartesian product is denoted by the "X" symbol. Let's say we have two relations R and S. Cartesian product will combine every tuple(row) from R with all the tuples from S. I know it sounds complicated, but once we look at an example, you'll see what I mean.
Notation: R X S
Where R is the first relation
S is the second relation

As we can see from the notation it is also a binary operator.

Let's combine the two relations STUDENT and EMPLOYEE.

. . . And so on.

Rename (ρ)

Rename operation is denoted by "Rho"(ρ). As its name suggests it is used to rename the output relation. Rename operator too is a binary operator.
Notation: ρ(R,S)
Where R is the new relation name
S is the old relation name

Let's have an example to clarify this
Suppose we are fetching the names of students from STUDENT relation. We would like to rename this relation as STUDENT_NAME.

STUDENT_NAME

As you can see, this output relation is named "STUDENT_NAME".

Takeaway

• Select (σ) is used to retrieve tuples(rows) based on certain conditions.
• Project (∏) is used to retrieve attributes(columns) from the relation.
• Union (∪) is used to retrieve all the tuples from two relations.
• Set Difference (-) is used to retrieve the tuples which are present in R but not in S(R-S).
• Cartesian product (X) is used to combine each tuple from the first relation with each tuple from the second relation.
• Rename (ρ) is used to rename the output relation.

Master structured AI Engineering + GenAI hands-on, earn IIT Roorkee CEC Certification at ₹40,000

Derived Operations

Also known as extended operations, these operations can be derived from basic operations and hence named Derived Operations. These include three operations: Join Operations, Intersection operations, and Division operations.

Let's study them one by one.

Join Operations

Join Operation in DBMS are binary operations that allow us to combine two or more relations.
They are further classified into two types: Inner Join, and Outer Join.

First, let's have two relations EMPLOYEE consisting of E_NO, E_NAME, CITY and EXPERIENCE. EMPLOYEE table contains employee's information such as id, name, city, and experience of employee(In Years). The other relation is DEPARTMENT consisting of D_NO, D_NAME, E_NO and MIN_EXPERIENCE.

DEPARTMENT table defines the mapping of an employee to their department. It contains Department Number, Department Name, Employee Id of the employee working in that department, and the minimum experience required(In Years) to be in that department.

EMPLOYEE

DEPARTMENT

Also, let's have the Cartesian Product of the above two relations. It will be much easier to understand Join Operations when we have the Cartesian Product.

Inner Join

When we perform Inner Join, only those tuples returned that satisfy the certain condition. It is also classified into three types: Theta Join, Equi Join and Natural Join.

Theta Join (θ)

Theta Join combines two relations using a condition. This condition is represented by the symbol "theta"(θ). Here conditions can be inequality conditions such as >,<,>=,<=, etc.
Notation : R ⋈θ S
Where R is the first relation
S is the second relation

Let's have a simple example to understand this.

Suppose we want a relation where EXPERIENCE from EMPLOYEE >= MIN_EXPERIENCE from DEPARTMENT.

Check the Cartesian Product, if in any tuple/row EXPERIENCE >= MIN_EXPERIENCE then insert this tuple/row in output relation.

Equi Join

Equi Join is a special case of theta join where the condition can only contain **equality(=)** comparisons.
A non-equijoin is the inverse of an equi join, which occurs when you join on a condition other than "=".

Let's have an example where we would like to join EMPLOYEE and DEPARTMENT relation where E_NO from EMPLOYEE = E_NO from DEPARTMENT.

Check Cartesian Product, if the tuple contains same E_NO, insert that tuple in the output relation

Natural Join (⋈)

A comparison operator is not used in a natural join. It does not concatenate like a Cartesian product. A Natural Join can be performed only if two relations share at least one common attribute. Furthermore, the attributes must share the same name and domain.
Natural join operates on matching attributes where the values of the attributes in both relations are the same and remove the duplicate ones.
Preferably Natural Join is performed on the foreign key.
Notation : R ⋈ S
Where R is the first relation
S is the second relation

Let's say we want to join EMPLOYEE and DEPARTMENT relation with E_NO as a common attribute.

Notice, here E_NO has the same name in both the relations and also consists of the same domain, i.e., in both relations E_NO is a string.

But unlike the above operation, where we have two columns of E_NO, here we are having only one column of E_NO. This is because Natural Join automatically keeps a single copy of a common attribute.

Hiring Partners:

GoogleAmazonMicrosoftFlipkartAdobe1200+ more

Become the Ai engineer who can design, build, and iterate real AI products, not just demos with an IIT Roorkee CEC Certification

Outer Join

Unlike Inner Join which includes the tuple that satisfies the given condition, Outer Join also includes some/all the tuples which don't satisfy the given condition. It is also of three types: Left Outer Join, Right Outer Join, and Full Outer Join.

Let's say we have two relations R and S, then
Below is the representation of Left, Right, and Full Outer Joins.

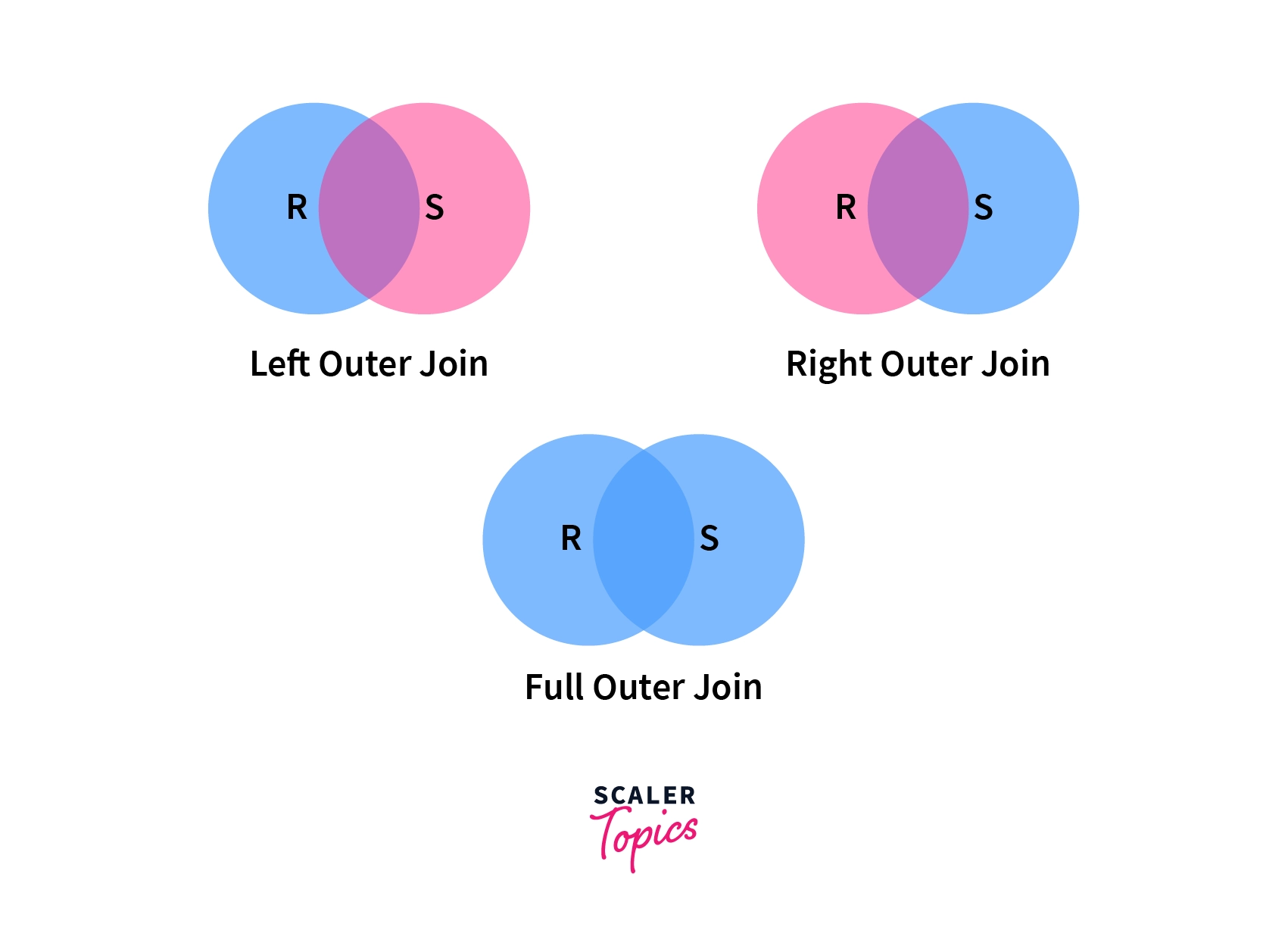
Left Outer Join

As we can see from the diagram, Left Outer Join returns the matching tuples(tuples present in both relations) and the tuples which are only present in Left Relation, here R.

However, if the matching tuples are NULL, then attributes/columns of Right Relation, here S are made NULL in the output relation.

Let's understand this a bit more using an example:

Here we are combining EMPLOYEE and DEPARTMENT relation with the constraint that EMPLOYEE's E_NO must be equal to DEPARTMENT's E_NO.

As you can see here, all the tuples from left, i.e., EMPLOYEE relation are present. But E-4 is not satisfying the given condition, i.e., E_NO from EMPLOYEE must be equal to E_NO from DEPARTMENT, still it is included in the output relation. This is because Outer Join also includes some/all the tuples which don't satisfy the condition. That's why Outer Join marked E-4's corresponding tuple/row from DEPARTMENT as NULL.

Right Outer Join

Right Outer Join returns the matching tuples and the tuples which are only present in Right Relation here S.

The same happens with the Right Outer Join, if the matching tuples are NULL, then the attributes of Left Relation, here R are made NULL in the output relation.

We will combine EMPLOYEE and DEPARTMENT relations with the same constraint as above.

As all the tuples from DEPARTMENT relation have a corresponding E_NO in EMPLOYEE relation, therefore no tuple from EMPLOYEE relation contains a NULL.

Full Outer Join

Full Outer Join returns all the tuples from both relations. However, if there are no matching tuples then, their respective attributes are made NULL in output relation.

Again, combine the EMPLOYEE and DEPARTMENT relation with the same constraint.

Intersection (∩)

Intersection operation is done by Intersection Operator which is represented by "intersection"(∩).It is the same as the intersection operator from set theory, i.e., it selects all the tuples which are present in both relations. It is a binary operator as it requires two operands. Also, it eliminates duplicates.
Notation : R ∩ S
Where R is the first relation
S is the second relation

Let's have an example to clarify the concept:
Suppose we want the names which are present in STUDENT as well as in EMPLOYEE relation, Relations we used in Basic Operations.

Division (÷)

Division Operation is represented by "division"(÷ or /) operator and is used in queries that involve keywords "every", "all", etc.
Notation : R(X,Y)/S(Y)
Here,
R is the first relation from which data is retrieved.
S is the second relation that will help to retrieve the data.
X and Y are the attributes/columns present in relation. We can have multiple attributes in relation, but keep in mind that attributes of S must be a proper subset of attributes of R.
For each corresponding value of Y, the above notation will return us the value of X from tuple<X,Y> which exists everywhere.

It's a bit difficult to understand this in a theoretical way, but you will understand this with an example.

Let's have two relations, ENROLLED and COURSE. ENROLLED consist of two attributes STUDENT_ID and COURSE_ID. It denotes the map of students who are enrolled in given courses.

COURSE contains the list of courses available.
See, here attributes/columns of COURSE relation are a proper subset of attributes/columns of ENROLLED relation. Hence Division operation can be used here.

ENROLLED

COURSE

Now the query is to return the STUDENT_ID of students who are enrolled in every course.

This will return the following relation as output.

Takeaway

• Theta Join (θ) combines two relations based on a condition.
• Equi Join is a type of Theta Join where only equality condition (=) is used.
• Natural Join (⋈) combines two relations based on a common attribute (preferably foreign key).
• Left Outer Join (⟕) returns the matching tuples and tuples which are only present in the left relation.
• Right Outer Join (⟖) returns the matching tuples and tuples which are only present in the right relation.
• Full Outer Join (⟗) returns all the tuples present in the left and right relations.

Read More:

• DBMS Keys.
• Integrity Constraints in DBMS.
• Relational model in DBMS.
• Glossary of DBMS.