Python Program to Print Fibonacci Series

What is Fibonacci Series?

We can define the Fibonacci series as a series of numbers that start from 0 & 1, and the next number can be generated by adding the last two preceding numbers.

Fibonacci Series Logic in Python

Example: 0, 1, 1, 2, 3, 5, 8

Fibonacci series starts with 0 and 1, so we consider these as the default values of the series.

The following number will be an addition of the last two numbers.

As you can see in the above diagram, The Fibonacci series started with 0 and 1 currently, which are the last two numbers and then by adding these values, we got 1. Now the last two values are (1,1). By adding them, we got 2. Now the last two numbers are (1,2), we add them to get the following number of the Fibonacci series, and It is done until the number of terms you want.

Fibonacci Series Formula in Python

So here, term 7 is called x7, which is equal to 13,

From the above diagram we can write the formula as: Xn = Xn-1 + Xn-2

Where:

• Xn is the n-th term.
• Xn-1 is the (n-1)-th term.
• Xn-2 Is the (n-2)-th term.

Implementing the Fibonacci Series in Python

In the implementation of the Fibonacci series, we are going to see the following points:

• Fibonacci series in python using recursion
• Fibonacci series in python using dynamic programming
• Fibonacci series in python – space-optimized
• Fibonacci series in python using while loop

Fibonacci series in python using Recursion

Any function calling itself is called Recursion. Using a recursive algorithm on specific problems is relatively easy rather than an iterative approach. But in this case, using recursion in the Fibonacci series is not a good idea because it takes exponential time complexity.

Let’s see how to print the Fibonacci series till the nth term.

Constraint: n>=1.

Python Code – Recursion

Output:

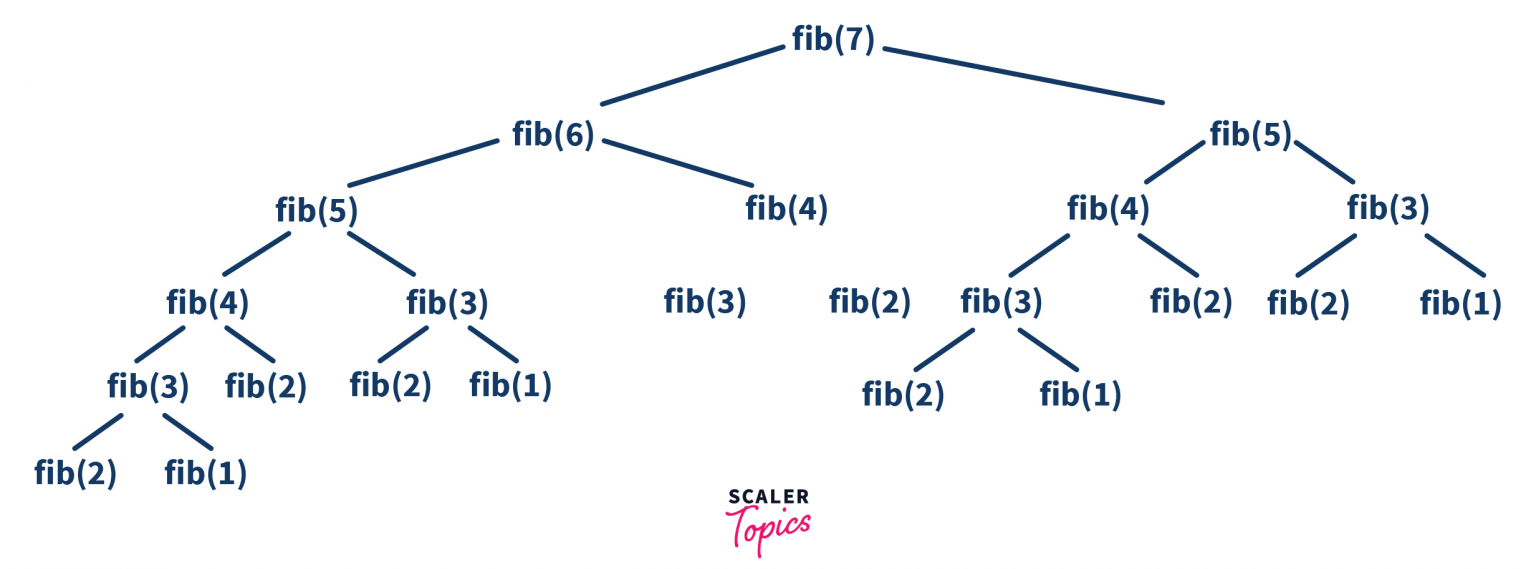
From the diagram below, we can see there is a lot of repetition of the functions. This means our program has calculated the same thing many times, which consumes too much time & space

Time Complexity: O(2^n)

Space Complexity: O(n) (Max depth of the recursion tree)

Let’s take an example. Suppose we have passed n = 7 to our function fib(7). Now we have to calculate for the last two values that is fib(7-1) + fib(7-2), which is fib(6) + fib(5), but when we calculate for fib(6), again fib(5) will be calculated as you can see in the below diagram.

''

So, it’s better to avoid this recursive approach in the Fibonacci series program.

Fibonacci series in python using dynamic programming

Dynamic Programming is an algorithmic technique that solves problems by breaking them into subproblems and saves the result of these subproblems so that we do not have to re-compute them when needed.

We can check if the subproblem is already solved, and then we can directly access the result and use it. It saves computation time.

Python Code – Dynamic programming

Output:

In the above code, we have overcome the problem of repeated work done By storing subproblems results into a list named ‘fib_series’.

We have calculated the following Fibonacci series number and stored it in the ‘next_number’ variable, stored in the fib_series list To remember the result.

Time Complexity: O(n)

Space Complexity: O(n)

Here, we have optimized the time complexity by dynamic programming, but still, space complexity is not optimized.

Fibonacci series in python – space optimized

Now let’s optimize the space complexity.

Python Code – Space Optimized

Output:

In the above code, we have not taken any extra space memory. We have printed the Fibonacci series using a for loop by which we can say it is space-optimized.

Here the space complexity is O(1) & time complexity O(n). We have separately printed the first two default values, which are 0 & 1 and with the help of these values, we have calculated the next sequence of the Fibonacci series.

Fibonacci series in python using while loop

Here, the Fibonacci series using a while loop is implemented.

Python Code:

Output:

Time Complexity: O(n)

Space Complexity: O(1)

So, we have discussed four methods to print the Fibonacci series in python. It is totally up to you which method you should use. If complexity does not matter, then you can use a recursive approach. Else, you can use a dynamic programming approach.

Some of the applications of the Fibonacci series:

1. Fibonacci search – It can be defined as a technique which is based on the comparison that uses Fibonacci numbers to search an element in a sorted array.

2. Golden Ratio – Fibonacci series helps to understand the golden ratio. The Golden ratio is derived from the Fibonacci series. The golden ratio describes a predictable pattern on everything from atoms to giant stars in space.

Invest in your programming future with our in-depth Dynamic Programming Course. Enroll now and supercharge your coding skills!

Read More:

• Factorial Program in Python
• Factorial Using Recursion in Python
• Fibonacci Series in Python Using Recursion