Recursion in Python

What is Recursion in Python?

What would happen if we placed two mirrors parallel to each other? You will see multiple images stretched to infinity caused by the reflections between the surfaces.

Imagine you want to know the name of a person in the queue that you are standing in. You ask people to find out about it.

They keep asking the next person until they find an answer. Once an answer is found, they send it back until it reaches you.

The above two examples depict a process in which a particular action is repeated until a condition is met. These processes have a strong resemblance to what we call recursion.

A process in which a function calls itself is called recursion. This process helps ease the method of solving problems by replacing iterative code with recursive statements.

Working of Recursion in Python

Imagine sitting in an auditorium and being confused about the row you are sitting in. Since you cannot count till the first bench, you ask the person right before you what row they are sitting in. If the person doesn’t know his seat number, he will ask the person right before him.

The process of asking will continue till someone knows their seat number. As shown in the above diagram, when the person in the 3rd row informs that he is sitting in row 3, the person behind him will add one and pass on his row number 4 to the person right after. The row number will be calculated in each row and will be passed on until it reaches you. Once it reaches you, add 1 to get your final row number.

That is precisely how recursion in Python works.

Use of Recursion in Python

Quite often, people wonder why we should use recursion when loops exist. Everything can be coded without recursion.

The difference between iteration and recursion is there is no sequential end to recursive code. It tests on a base condition and can go on as long as that is satisfied.

Recursion is used in Python when problems can be broken into simpler parts for easier computation and more readable code.

For example, if you want to search for a student in a school, there would be two ways to do so. You could gather all the students in an auditorium and then search for her one by one. A more straightforward method would divide the school into sections until the smallest section could be made to find the student, i.e., it would make more sense to first search for the grade she is in, then the class, and then you'll be able to find her location much more easily.

Although recursion is found to give results faster in some cases when properly optimized, it can also add to memory usage.

Thus, recursion should be used only when needed.

Recursive Function in Python

In Python or any other programming language, recursion is a process in which a function calls itself. Such functions are called recursive functions.

In the auditorium example given above, we would have a recursive function called divide_and_search(), which takes the group of students. Based on the presence or absence of students in a section, the recursive function will run again at the invocation of the function each time, reducing the interval between the students.

It means that when the recursive function is first called where all the participants in the auditorium are placed, we will check if the student is present on a particular side of the auditorium.

If the student is present on the left, where only the odd grade students sit, we will now pass the odd grade students to the recursive function. At the following invocation, the student will be searched within the odd grades to find which particular grade she is in.

This process will continue until the required student is found.

Recursive function in Python has two parts:

(a) Base Case - This helps us to terminate the recursive function. It is a simple case that can be answered directly and doesn't use recursion. If satisfied, it returns the final computable answer. If this is omitted, the function will run till infinity.

(b) General (Recursive) Case - This case uses recursion and is called unless the base condition is satisfied.

Syntax:

The base case and its solution must first be identified to write a recursive function. More than one base case can be used depending on the situation. Once a base case has been identified, the general or recursive case has to be identified so that each recursive call takes us one step closer to achieving the base case.

A recursive function makes use of a call stack. Every time the recursive function gets called, that function gets added to the top of this stack. Imagine opening up an onion and you place every layer you peel near it. So, each layer, peeled, would be placed at the top of this peel stack.

Now compare this to a recursive function. Peeling each layer would be a recursive function call. When the first layer is peeled, the first peel() would be added at the top of the stack, then the next would be added above it, and so on, until the process is completed.

Example of Recursive Function

Suppose you want to find the sum of n natural numbers in python. We would write the following code to get the answer.

Output:

Working: When we call the function sum() with any positive integer, say 6, it will recursively call itself by decreasing the number. As shown in the recursive case, each function call adds the number argument with the value of the sum of the decremented number as given below:

$sum(6) = 6 + sum(5)$ $= 6 + 5 + sum (4)$ $= 6 + 5 + 4 + sum (3)$
$= 6 + 5 + 4 + 3 + sum (2)$
$= 6 + 5 + 4 + 3 + 2 + sum (1)$
$= 6 + 5 + 4 + 3 + 2 + 1$
$= 21$

Let’s understand this better through the step-by-step process diagram below. The recursive process starts when sum(6) is called and ends when we move into the base case, i.e., when sum (1) returns 1. Once this value is returned, it is added to all the values in the call stack as shown and finally, the value 21 is returned.

All recursive functions have two distinct phases of working - the winding and unwinding phases. The winding phase embarks with the recursive function being called the first time and moves ahead until the last recursive call. In this phase, no return statements are executed. The winding phase terminates when the base case's condition becomes true in a call.

That's when the unwinding phase begins. In this phase, all recursive functions return in the reverse order till the first instance of the function returns.

Types of Recursion in Python

There are mainly 2 types of recursive functions:

• Direct Recursion
• Indirect Recursion

1) Direct Recursion

In this type of recursion, the function calls itself.

a) Tail Recursion - A recursive call is said to be tail-recursive if it is the last statement to be executed inside the function.

Example of a Tail Recursive Call

The following function prints natural numbers from n in descending order. It is done by traversing digits from n to 1 and returning each digit at a call. In this example, the position of the print statement holds the utmost significance. The base case would be 0, where no value would be returned to the call.

In the first invocation of the function, the print statement causes 5 to be displayed on the screen, and disp(4) is added at the top of the stack. In the next invocation, 4 is printed, and disp(5) is added to the stack.

Similarly, 3, 2, and 1 are printed in the following invocations. In the last call, the value of n becomes 0, and thus the base case is satisfied, causing recursion to terminate.

Output:

Example of a Call That is Not Tail-Recursive

The following function is used to print natural numbers up to n in ascending order. Compared to the previous example, the print statement occurs after the recursive call in this function. So, the print statements come into play only during the unwinding phase.

At consecutive invocations of the function, disp(5), disp (4), disp(3), disp(2), disp (1) are added to the top of the stack, respectively. When we encounter disp(0), the terminating condition is satisfied, returning the function. At this point, the unwinding phase begins. The calls return in reverse order, with disp(1) returning first, followed by the rest.

Thus, the print statement of disp(1) occurs before. So, the values are printed in ascending order.

Output:

In non-void functions, if the recursive call appears in the return statement and is not part of the expression, the call is tail-recursive.

Example of a Tail-Recursive Call

The following function is used to calculate the GCD of 2 given numbers. As we know, if the smaller number is 0, then the GCD of the two numbers would be the larger number. This is the base case of our problem.

By Euclid’s Remainder Algorithm, we know that:

$GCD (a,b)= GCD (b, a/b)$

Consider a=49 and b=35, then

$GCD(49,35) = GCD (35, 14)$
$= GCD (14, 7)$
$= GCD (7, 0)$
$= 7$

The code for this is as given below:

Output:

Example of a Call that is Not Tail-Recursive

The following function is used to calculate the factorial of a given number. Although the call seems to be tail-recursive due to the presence of the function name in the return statement, it is not because the call is a part of an expression in this case. In this example, the base case is when the number is 0, and the value one is returned.

The general formula for factorial is-

$n! = n * n-1 * n-2 * ….. * 1$

Thus at each recursive call, the current n would be multiplied by the factorial of the previous number.

Output:

If, in a recursive function, all the calls in it are tail-recursive, then it is called tail recursion. In tail-recursive functions, the last task done by the function is a recursive call, so there is no operation pending after the recursive call occurs. Consider the following function, which displays the first 5 natural numbers in reverse order.

Output:

b) Head Recursion

If in a recursive function, the last statement is not a recursive call, i.e., during the unwinding phase, there are still some steps to occur, then it is called head recursion.

Consider the following function, which displays the first five natural numbers in ascending order. At consecutive invocations of the function, headr(5), headr(4), headr(3), headr(2), headr(1) are added to the top of the stack, respectively. When we encounter headr(0), the terminating condition is satisfied, returning the function.

At this point, the unwinding phase begins. The calls return in reverse order, with headr(1) returning first, followed by the rest. Thus, the print statement of headr(1) occurs before. So, the values are printed in ascending order.

Output:

2. Indirect Recursion

In this type of recursion, the function calls another function which calls the original function. Here, when function A() is called, it first executes the print statement and then calls function B() with an incremented value of n. Its print statement is executed within function B, and then the function A() with a value of n reduced by five is called.

The process continues as long as the terminating condition is not satisfied.

Output:

The chain of functions in indirect recursion may involve any number of functions. We can have f1() call f2() that calls f3() that calls f4() that calls f5() that in turn calls f1(). The usage of indirect recursion increases the complexity of code and is thus not very common.

Recursion in Python with Numbers

Recursion is very commonly used to compute operations on numbers. Some of the most common examples are finding the factorial of a number, displaying or calculating the sum of a series of numbers, reversing integers, and testing for divisibility.

Let’s see some examples to understand this in more detail.

1. Divisibility by 7

The rule for divisibility by 7 involves taking the last digit of the number, doubling it, and then subtracting this value from the rest of the number. If the result is a multiple of 7 (including 0), then the original number is divisible by 7.

Given a number in the format (10a + b), where (b) is the unit digit, and (a) is the number divided by 10 (essentially the number without its last digit), the divisibility rule can be applied as follows:

If (10a + b) is divisible by 7, then instead of checking if (2(10a + b)) is divisible by 7 (which is an incorrect step), you should:

1. Double the unit digit ((b)).
2. Subtract this doubled value from the remaining part of the number ((a)).
3. Check if the result is divisible by 7.

The correct formula from the provided steps should be: [a - 2b]

This means if (a - 2b) is divisible by 7, then (10a + b) is also divisible by 7.

For the example with the number 798:

• (a = 79), (b = 8)
• Applying the rule: (79 - 2 \times 8 = 79 - 16 = 63), which is divisible by 7. Thus, 798 is divisible by 7.

Our recursive approach will be:

• Start with the given number. If it's negative, make it positive.
• Apply the rule (a - 2b) recursively, where (a) is the number without its last digit and (b) is the last digit.
• If during the recursion, the number becomes 0 or 7, return True.
• If the number reduces to a value less than 10 and is not 0 or 7, return False.

Code:

Output:

2. Factorial of a Number

Factorial is the product of all numbers smaller than or equal to the given number.
For example, Factorial of $5 = 5 * 4 * 3 * 2 * 1 = 120$ In this example, the base case is when the number is 0, and the value 1 returns. The general formula for factorial is given as:

$n! = n * n-1!$ $= n* n-1 * n-2 * ….. * 1$

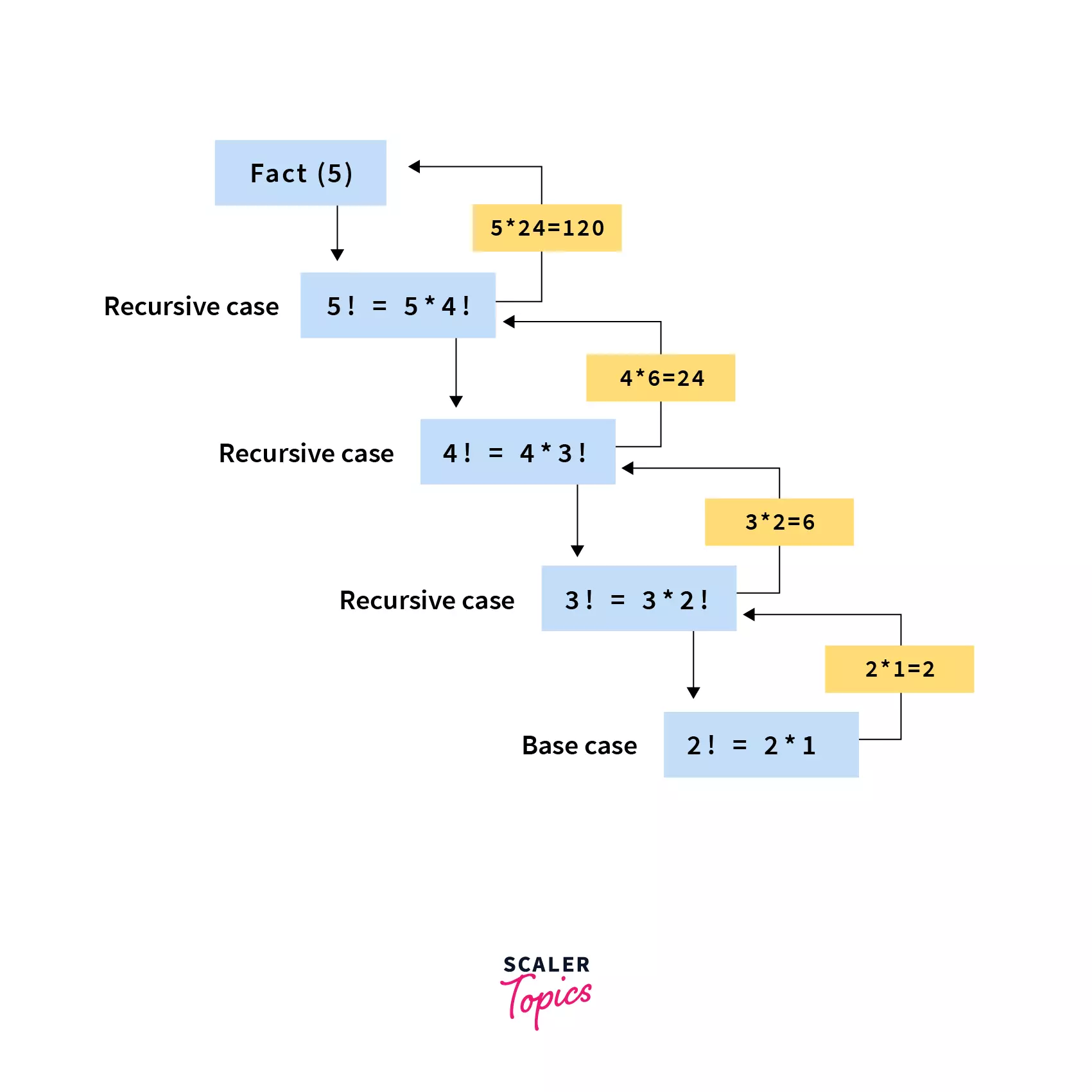
Thus at each recursive call, the current n would be multiplied by the factorial of the previous number. So, the factorial of 5 would be calculated as follows:

$fact(5) = 5 * fact (4)$
$= 5 * 4 * fact(3)$
$= 5 * 4 * 3 * fact(2)$
$= 5 * 4 * 3 * 2 * fact (1)$
$= 5 * 4 * 3 * 2 * 1$
$= 120$

The above working can be better understood by the diagram below:

Code:

Output:

3. To find the nth Number in Fibonacci Series

Fibonacci series is a series starting in 0,1 in which a number can be calculated as the sum of the previous two numbers. A 10-number Fibonacci series would be as follows:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34

The problem of finding the nth Fibonacci series can be recursively defined as:

Base Case:

• When n=0, the value returned would be 0
• When n=1 or n=2, the value returned would be 1

Recursive Case:.

Find the sum of the previous 2 numbers using a recursive call given by:

$fib(n-1) + fib(n-2)$

Code:

Output:

4. Integer Reversal

We read all the numbers from right to left to reverse an integer, i.e., from units place and backward.
E.g., The reverse of 765 is 567.

Algorithm:

1. Initialize a variable called res to 0.
2. If the given integer is greater than 0 a. Add res*10+remainder of the number to res. b. Divide the number by 10

If we have to find the reverse of 524, we can proceed as:

Code:

Output:

Recursion in Python with Strings and Arrays

A string in Python can be defined recursively as:

1. An empty string.
2. A character is followed by a string smaller than the original string by 1 character.

Similarly, an array in Python can be defined recursively as:

1. An empty array.
2. An array element is followed by an array smaller than the original array by 1 array element.

These are the major principles we will consider while solving problems in recursion for strings and arrays.

Recursion for strings and arrays is widely used for sorting, reversing, calculating the number of elements that satisfy a given condition, and evaluating series.

Following are some examples that will help you better understand how recursion can be used in arrays and strings in Python.

1. Ascending or Not

Consider you are given an array of integers ordered randomly. You are asked to check if the array is in ascending order, i.e., increasingly with the smallest number placed first and the other numbers following it. To implement a solution for this problem, given a string, we have first to calculate the length of the given array. As discussed in the recursive definition of an array, we consider 2 cases:

• Base case:
  • Array of Length 0 - Empty Array (Need not be sorted)
  • Array of Length 1 - Array with only one element (Already Sorted)

In both these cases, we do not need to sort the array further, and thus return a True value.

• Recursive Case - This is triggered when our array has more than one element. So, we compare pairs of elements at each invocation of the recursive call and recursively call the next invocation as follows:
  • arr[0] <= arr [1] and isAscending(arr[1:])

So, at the first invocation, the elements at positions 0 and 1 are compared, and the AND value of this and the comparison of the next elements of the array is returned.

At the end of the unwinding phase, a True value is returned only if the entire array is in ascending order. Let us consider an array: 1, 2, 3, 4 5. The operations take place as follows:

• 1 < = 2 and isAscending(2,3,4,5)
• True and 2<=3 and isAscending(3,4,5)
• True and True and 3<=4 and isAscending(4,5)
• True and True and True and 4<=5 and True
• True

Code:

Output:

2. Number of Vowels

Given a string, we must calculate the number of vowels present in it. For this, we will use two functions: isVowel() to check whether the character in consideration is a vowel and countVowels() , a recursive function used to count the number of vowels present in the string. When the countVowels function is called, we pass the string and its length.

Considering the recursive definition of a string, as mentioned earlier, the smallest string that can contain vowels would be one character long. If the string is one character long, we check if it is a vowel by calling the isVowel() function.

In the comparison, the character is first converted to uppercase before comparing to reduce the number of comparisons between different cases of the same vowel. For a string with more than one character, we check whether the last character is a vowel and if it is, add 1 to the value returned by passing the string after the elimination of the last character to the countVowels() function.

Suppose we have been given the string ‘Eat’. After the first invocation, we will apply countVowels to the string ‘Ea’. Since ‘t’ is not a vowel, the number of vowels, for now, is 0.

After the second invocation, we will apply countVowels() to the string ‘E’. Since ‘a’ is a vowel, the number of vowels will now be incremented to 1.

After the third invocation, we call the isVowel() function for E. Since ‘E’ is a vowel, the number of vowels will now be changed to 2. The final value, 2 is now returned.

Code:

Output:

3. Palindrome

A palindrome is a word or sequence of numbers/characters that read the same way backward as they read forwards.

Examples of palindromes are 12321 and Malayalam. As discussed in the recursive definition of a string, we consider 2 cases:

• Base case - String of Length 1 - String with only one character. It is a palindrome, and thus, we return a True value.
• Recursive Case - This is triggered when our string has more than one character. So, we compare pairs of characters at the two extremes of the string at each invocation of the recursive call and recursively call the next invocation as follows:
  str[0] == str[-1]andisPalindrome(arr[1: -1])

Here, str[-1] represents the last character in the string. So, at the first invocation, the characters at positions 0 and n-1 (where n= the length of the string) are compared. And the AND value of this and the comparison of the following characters of the string is returned.

At the end of the unwinding phase, a True value is returned only if all comparisons return True.

Consider the string ‘ABA’. The operations take place as follows:

• A == A and isPalindrome(str[1:-1])
• True and True
• True

Code:

Output:

4. Reversal of String

Given a string, we need to reverse it, i.e., print the string from right to left (end to the start). We consider 2 cases to solve this problem:

• Base case: If the string is empty, i.e., its length is 0, we return from the function.

• Recursive case: This case executes until the string has characters. Here, we assign the string's first character to a temporary variable and call the strRev() function for the remaining part of the string.

Once the string is empty, the unwinding phase begins. It starts with printing the last character in the string and moves backward till all the characters are printed on the screen. The final output thus contains the string in reverse order.

Suppose that the string to be reversed is ‘Hello’. Then the winding and unwinding phases will be carried out as follows:

Code:

Output:

Recursion in Python with Data Structures

Data in Python can be stored and organized more efficiently using data structures. Various structures are used based on the purpose being served. These data structures decide the operations that can take place on the data.

We can recursively define a data structure in Python in terms of itself. It helps us take advantage of the recursive structure; thus, they can be naturally implemented using recursive functions. This type of recursion is called structural recursion. Let's see two examples to understand how recursion is implemented in Python for linked lists and trees.

1. Inserting a Node at the End and Traversing a Linked List Using Recursion

In Python, a data sequence can be connected using links (in the form of a pointer) to save memory. Unlike arrays, linked lists allocate memory only for values to be stored, thus avoiding any wastage of memory.

A linked list in Python is recursively defined as:

1. An empty linked list.
2. A node followed by a linked list smaller than the original linked list by one node.

To insert a node at the end of a linked list, we need to traverse the linked list until the final element, i.e., the link of the element, is a null value (None). The following example shows recursive functions used for the insertion and traversal of the linked list.

Output:

In the above code, first, a node class is defined. It contains the data held by a node and the link to the next element. Initially, the next element is considered to be None.

During the first allocation, an object of the node class is instantiated with the value for the data. Since the first node will also be the last node of the linked list at that time, the next holds a None value.

To insert a new node at the end of a linked list:

1. Base Case: If the linked list is empty or we have reached the last node, i.e., if the object's value is None, allocate a new node by calling the NewNode() function.
2. General Case: If the linked list is not empty, it calls the insertEnd() function.

To traverse the linked list:

1. Base Case: If the list is empty, i.e., you return to the main if the object has a None value.
2. General Case: Print the data in the current node. And then call the traverse() function for the link of the current node.

2. Inorder Traversal of Binary Tree

A binary tree can have up to 2 children, the left one and right one being called the left child and right child, respectively.

A binary tree in Python is a finite set of nodes that can be recursively defined as:

1. An empty tree.
2. A tree that consists of a distinguished node called root, and the remaining nodes are partitioned into two disjoint sets, both binary trees.

Unlike linear data structures, we can traverse binary trees in different ways. Inorder Traversal of the Binary tree returns the left child (and its entire subtree), followed by the parent node, and then the right child (and its entire subtree). We commonly use recursion to traverse binary trees as they are implemented using a stack.

Code:

Output:

In the above code, a class node is defined first. This class node represents a node and contains the data it holds and links to the left and right children if any. The recursive function for the traversal is passed the address of the root node.

The inorder function works as follows:

1. Base case: If the root is empty, it returns to the code.
2. General Case:.
   • A recursive call is used to traverse the left subtree by accessing the current node's left child.
   • The current node is printed.
   • A recursive call is used to traverse the right subtree by accessing the right child of the current node.

In the main, the objects are assigned to values of nodes as given in the above image.

Advantages and Disadvantages of Recursion in Python

Advantages

1. Recursion in Python often reduces the length of the code.
2. It helps increase the elegance and conciseness of the code.
3. It helps in breaking a complex problem into simpler ones.
4. We can do sequence generation and tree traversal better and easily with recursion.

Disadvantages

1. It is difficult to frame and understand the logic behind recursive functions. Thus, making them hard to debug.
2. Recursion in Python uses more memory as values need to be added to the call stack with each recursive call.
3. Recursion in Python can be slow if not implemented correctly.
4. Python Recursive calls can be inefficient as, in some cases, they take up a lot of memory and time.

Read More

• Queue in Python.
• Factorial using Recursion
• Python Stack.
• Sum of Digits of a Number in Python.
• Sum of Prime Numbers in Python.