Dining Philosophers Problem in OS
Overview
The dining philosophers problem is a classic operating-system synchronisation puzzle in which five philosophers sit around a table sharing five forks, and each needs both neighbouring forks to eat. The problem was originally formulated by Edsger Dijkstra. It models how concurrent processes compete for limited shared resources, and it is used to demonstrate deadlock, starvation, and mutual exclusion.
The problem arises when multiple processes need to access limited shared resources at the same time. Without proper synchronization, sharing a resource between processes can lead to data inconsistency.
Dining Philosophers Problem in OS
Consider two processes P1 and P2 executing simultaneously, while trying to access the same resource R1, this raises the question of who will get the resource and when. This problem is solved using process synchronization.
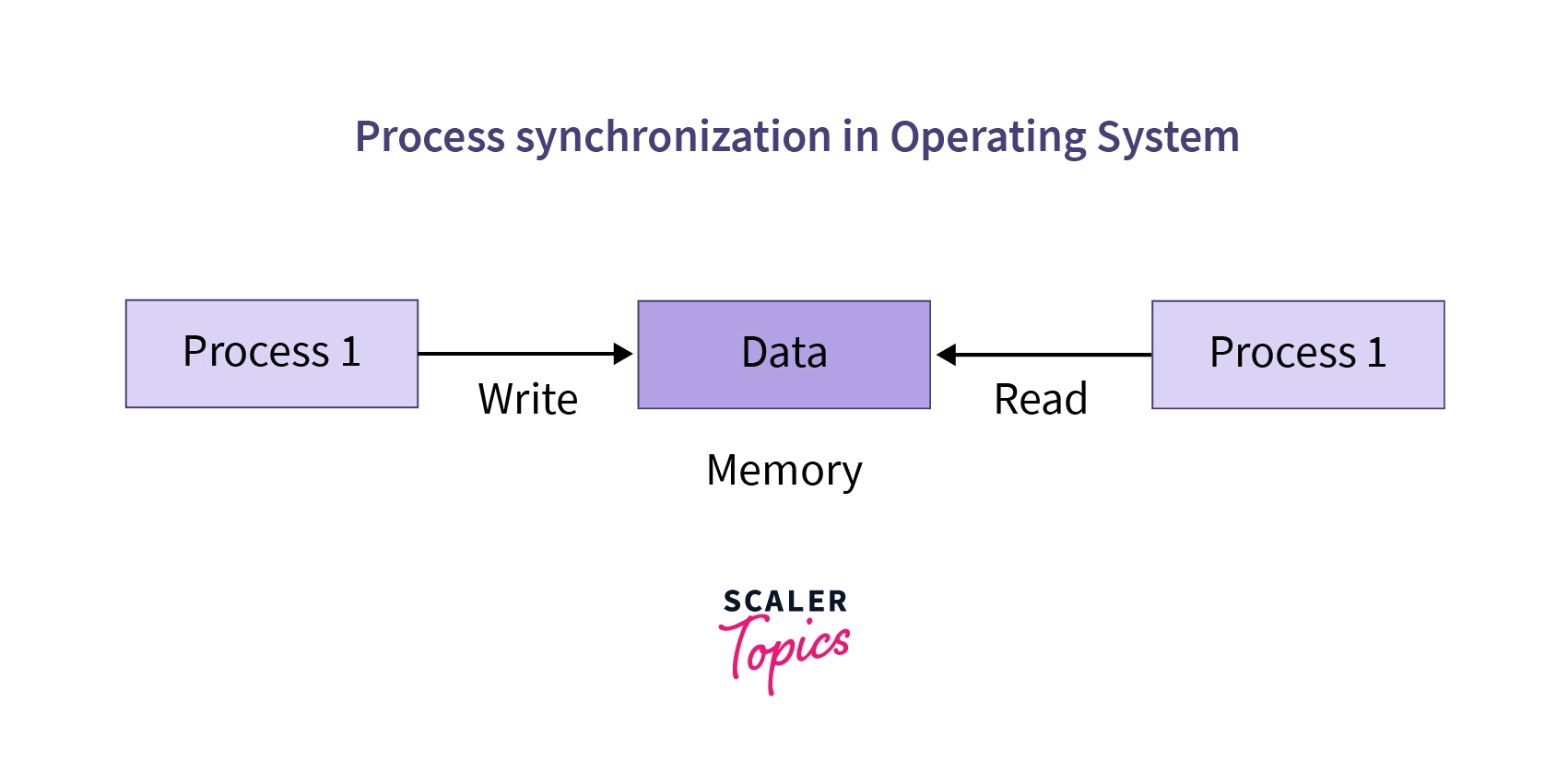
The act of synchronizing process execution such that no two processes have access to the same associated data and resources are referred to as process synchronization in operating systems.
It's particularly critical in a multi-process system where multiple processes are executing at the same time and trying to access the very same shared resource or data.
This could lead to discrepancies in data sharing. As a result, modifications implemented by one process may or may not be reflected when the other processes access the same shared data. The processes must be synchronized with one another to avoid data inconsistency.
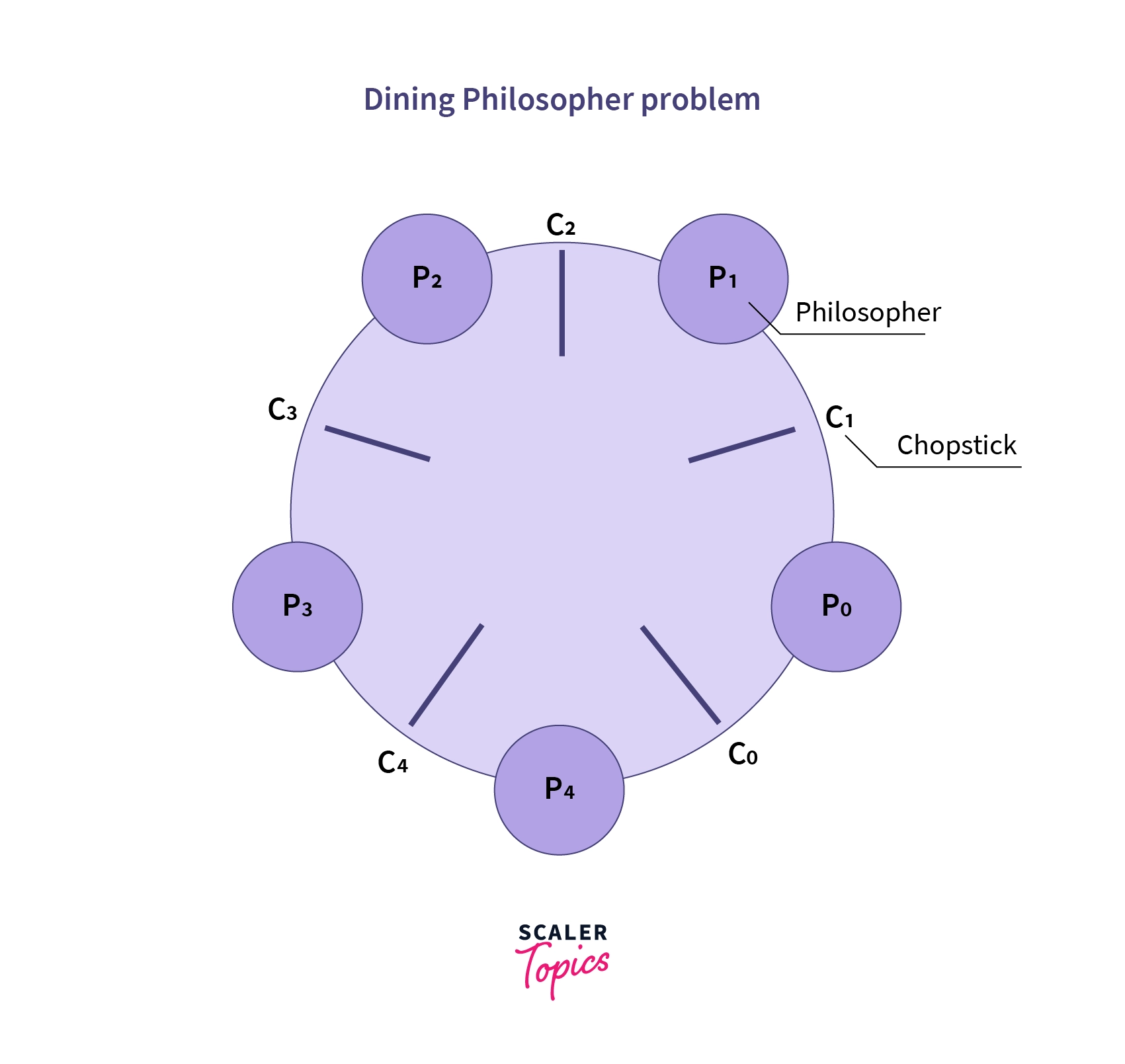
And the Dining Philosophers Problem is a typical example of limitations in process synchronization in systems with multiple processes and limited resources. According to the Dining Philosopher Problem, assume there are K philosophers seated around a circular table, each with one chopstick between them. This means, that a philosopher can eat only if he/she can pick up both chopsticks next to him/her. One of the adjacent followers may take up one of the chopsticks, but not both.
For example, let’s consider P0, P1, P2, P3, and P4 as the philosophers or processes and C0, C1, C2, C3, and C4 as the 5 chopsticks or resources between each philosopher. Now if P0 wants to eat, both resources/chopsticks C0 and C1 must be free, which would leave P1 and P4 void of the resource and the process wouldn't be executed, which indicates there are limited resources(C0,C1..) for multiple processes(P0, P1..), and this problem is known as the Dining Philosopher Problem.
:::
Build an AI-First Career, Master the Complete Skillset
Choose from our industry-leading programs designed for career success
Modern Software and AI Engineering Program
Master full-stack development with AI integration
+1000 moreModern Data Science and ML with specialisation in AI
Advanced data science techniques with AI specialization
+1000 moreAdvanced AIML with Specialisation in Agentic AI
Deep dive into AIML with focus on Agentic systems
+1000 moreDevOps, Cloud & AI Platform Engineering
Build and manage AI-powered cloud infrastructure
+1000 moreAI Engineering Advanced Certification by IIT-Roorkee
Premier AI engineering certification from IIT-Roorkee
AI Forward Deployed Engineer Program
Full-stack engineering, production AI and client-facing consulting
+1000 moreThe Solution of the Dining Philosophers Problem
The solution to the process synchronization problem is Semaphores, A semaphore is an integer used in solving critical sections.
The critical section is a segment of the program that allows you to access the shared variables or resources. In a critical section, an atomic action (independently running process) is needed, which means that only a single process can run in that section at a time.
Semaphore has 2 atomic operations: wait() and signal(). If the value of its input S is positive, the wait() operation decrements, it is used to acquire resources while entry. No operation is done if S is negative or zero. The value of the signal() operation's parameter S is increased, it is used to release the resource once the critical section is executed at exit.
Here's a simple explanation of the solution:
Explanation:
- The wait() operation is implemented when the philosopher is using the resources while the others are thinking. Here, the threads use_resource[x] and use_resource[(x + 1) % 5] are being executed.
- After using the resource, the signal() operation signifies the philosopher using no resources and thinking. Here, the threads free_resource[x] and free_resource[(x + 1) % 5] are being executed.
This approach appears to provide a way for each philosopher to acquire the two required chopsticks before eating. However, when every philosopher picks up the left chopstick first and then waits for the right one, each can end up holding one chopstick while waiting for the other. This creates a deadlock, so this first attempt does not work.
We will run the array of philosophers in parallel to execute the critical section (dine ()), the critical section consists of thinking, acquiring two chopsticks, eating and then releasing the chopsticks.
C program:
Output
Let's Understand How the Above Code is Giving a Solution to the Dining Philosopher Problem?
We start by importing the libraries pthread for threads and semaphore for synchronization. And create an array of 5 p_threads representing the philosophers. Create an array of 5 mutexes representing the chopsticks.
The pthread library is used for multi-threaded programming which allows us to run parallel sub-routines using threads. The <semaphore.h> header is used to perform semaphore operations.
We initialise the counter i and status message variable as int and a pointer msg, and intialise the semaphore array.
We create the philosopher threads using pthread_create and pass a pointer to the dine function as the subroutine and a pointer to the counter variable i.
All the philosophers start by thinking. We pass chopstick(n) (left) to pthread_mutex_lock to wait and acquire lock on it.
Then the thread waits on the right((n+1) % NUM_CHOPSTICKS) chopstick to acquire a lock on it (pick it up).
When the philosopher successfully acquires lock on both the chopsticks, the philosopher starts dining (sleep(3)).
Once the philosopher finishes eating, we call pthread_mutex_unlock on the left chopstick (signal) thereby freeing the lock. Then proceed to do the same on the right chopstick.
We loop through all philosopher threads and call pthread_join to wait for the threads to finish executing before exiting the main thread.
We loop thorough the chopstick array and call pthread_mutex_destroy to destroy the semaphore array.
The Drawback of the Above Solution of the Dining Philosopher Problem
Through the above discussion, we established that no two nearby philosophers can eat at the same time using the aforementioned solution to the dining philosopher problem. The disadvantage of the above technique is that it may result in a deadlock situation. This occurs when all of the philosophers choose their left chopstick at the same moment, resulting in a stalemate scenario in which none of the philosophers can eat, and hence deadlock will happen.
We can also avoid deadlock through the following methods in this scenario -
-
The maximum number of philosophers at the table should not exceed four, let’s understand why four processes is important:
- Chopstick C4 will be accessible for philosopher P3, therefore P3 will begin eating and then set down both chopsticks C3 and C4, indicating that semaphore C3 and C4 will now be increased to one.
- Now that philosopher P2, who was holding chopstick C2, also has chopstick C3, he will place his chopstick down after eating to allow other philosophers to eat.
-
The four starting philosophers (P0, P1, P2, and P3) must pick the left chopstick first, then maybe the right, even though the last philosopher (P4) should pick the right chopstick first, then the left. Let's have a look at what occurs in this scenario:
- This will compel P4 to hold his right chopstick first since his right chopstick is C0, which is already held by philosopher P0 and whose value is set to 0, i.e. C0 is already 0, trapping P4 in an unending loop and leaving chopstick C4 empty.
- As a result, because philosopher P3 has both left C3 and right C4 chopsticks, it will begin eating and then put down both chopsticks once finished, allowing others to eat, thereby ending the impasse.
-
If the philosopher is in an even position, he/she should choose the right chopstick first, followed by the left, and in an odd position, the left chopstick should be chosen first, followed by the right.
-
Only if both chopsticks (left and right) are accessible at the same time should a philosopher be permitted to choose his or her chopsticks.
Unlock the secrets of operating systems with our Operating System free course. Enroll now to get a comprehensive overview of their role and functionalities.
Deadlock vs Starvation
Deadlock and starvation both leave a process waiting, but the cause and system behaviour are different.
-
Deadlock: A set of philosophers becomes permanently blocked because each is waiting for a chopstick held by another philosopher in the same set. No philosopher in that cycle can proceed, so the system makes no progress for those processes.
-
Starvation: A philosopher remains unable to eat while other philosophers continue to acquire chopsticks and make progress. There is no circular wait involving every blocked philosopher; instead, one process can be repeatedly bypassed. The producer consumer problem also involves processes competing for shared resources.
In the Dining Philosophers Problem, the naive left-chopstick-first approach can produce deadlock when all five philosophers pick up their left chopstick and wait for their right one. The four fixes above remove this deadlock scenario, but they do not guarantee that access to both chopsticks will be distributed fairly.
For example, changing the order in which philosophers pick up chopsticks can prevent circular waiting, but a philosopher may still repeatedly lose access to a required chopstick as its neighbours continue eating. That is starvation, not deadlock. Preventing starvation requires an additional fairness property, such as bounded waiting or a fair queue for resource access. CPU scheduling algorithms can lead to starvation when a process keeps waiting while other processes are repeatedly given CPU time.
The Four Coffman Conditions
A deadlock can occur only when all four Coffman conditions hold at the same time. The Dining Philosophers Problem provides a direct example of each condition:
| Coffman condition | How it appears in the Dining Philosophers Problem |
|---|---|
| Mutual exclusion | Each chopstick can be held by only one philosopher at a time. A philosopher holding a chopstick prevents its neighbours from using it. |
| Hold and wait | A philosopher can hold one chopstick while waiting for the other chopstick needed to eat. |
| No preemption | A chopstick cannot be forcibly taken from a philosopher. It is released only when that philosopher finishes using it. |
| Circular wait | Each philosopher can hold one chopstick and wait for the next chopstick around the table, creating a cycle: P0 waits for P1, P1 waits for P2, and so on until P4 waits for P0. |
When all four conditions exist together, the philosophers can become permanently blocked. This is why the problem is useful beyond the table-and-chopsticks example: it demonstrates how competing processes can satisfy the conditions required for a deadlock.
These conditions also explain why deadlock avoidance techniques focus on preventing at least one of the conditions from holding.
How Scaler Transformed Careers in Different Fields
Scaler learners achieved 2.5x salary growth with average post-Scaler CTC reaching ₹23L.
Google
Amazon
Microsoft
Flipkart
Adobe1200+ moreComparison of Dining Philosophers Solutions
The naive approach fails because all five philosophers can acquire their left chopstick and then wait indefinitely for the right one. Each alternative breaks that situation differently: some restrict how many philosophers can compete, some change the order of acquisition, and others control whether a philosopher can hold only one chopstick. The difference becomes clearer when deadlock and starvation are considered separately.
| Approach | How it works | Deadlock-free? | Starvation-free? | Trade-off |
|---|---|---|---|---|
| Naive (left then right) | Everyone takes the left fork first | No | No | Simplest to write, but can deadlock |
| At most N−1 at the table | A counting semaphore seats only 4 of 5 | Yes | No | One extra semaphore; slightly less parallelism |
| Asymmetric (odd/even) | Even philosophers take the right fork first | Yes | No | No extra state at all; cheapest correct fix |
| One philosopher reversed | Only the last philosopher swaps order | Yes | No | Minimal change; asymmetry is easy to miss in review |
| Both-or-neither | Acquire both forks atomically or none | Yes | No | Requires atomic coordination of fork pickup |
| Waiter/arbitrator | A central waiter grants permission to eat | Yes | Yes, if the waiter serves FIFO | The waiter is a bottleneck and a single point of failure |
The table also shows why deadlock-free and starvation-free cannot be treated as the same result. Changing the order of chopstick acquisition is enough to remove the circular wait, but it does not decide which philosopher gets the resources next. A fairness rule, such as FIFO service by a waiter, is needed when the goal is to guarantee that waiting philosophers are eventually served.
Conclusion
- Process synchronization is defined as ensuring that no two processes have access to the same associated data and resources.
- The Dining Philosopher problem is an example of a process synchronization problem.
- The philosopher is an analogy for a process and a chopstick for resources; we can try to solve process synchronization problems using this.
- The naive solution can lead to a deadlock when each philosopher holds one chopstick and waits for the other. This is a drawback of the naive solution, not of the Dining Philosophers Problem itself.
- A solution can be deadlock-free without being starvation-free. Avoiding deadlock does not guarantee that every philosopher will get a fair chance to eat.
Interested in exploring this further? Scaler's free Operating System course covers process synchronisation, semaphores, and deadlock with practical examples.
FAQs
Turn Learning into Career Growth
1. What causes deadlock in the Dining Philosophers Problem?
Deadlock occurs when all five philosophers pick up their left chopstick and wait for their right chopstick. Each philosopher holds one resource while waiting for another, creating a circular wait. Since no philosopher can acquire both chopsticks, none can proceed to eat, and the system remains blocked.
2. How can the Dining Philosophers Problem be solved?
The Dining Philosophers Problem can be solved by changing how philosophers acquire chopsticks or by controlling access to them. Common approaches include allowing at most four philosophers to compete at once, reversing the pickup order for one or more philosophers, requiring both chopsticks together, or using a waiter.
3. What is the difference between deadlock and starvation in the Dining Philosophers Problem?
Deadlock means a group of philosophers becomes permanently blocked because each is waiting for a resource held by another. Starvation occurs when one philosopher keeps waiting while others continue eating. A solution can therefore prevent deadlock without guaranteeing that every philosopher receives fair access to the chopsticks.
4. What are the four Coffman conditions for deadlock?
The four Coffman conditions are mutual exclusion, hold and wait, no preemption, and circular wait. In the Dining Philosophers Problem, each chopstick can be held by one philosopher, a philosopher can hold one while waiting for another, chopsticks cannot be forcibly taken, and philosophers can form a circular waiting chain.
5. Is the Dining Philosophers Problem a starvation problem or a deadlock problem?
It can demonstrate both deadlock and starvation. The naive left-then-right approach can produce deadlock when every philosopher holds one chopstick and waits for another. Even after deadlock is prevented, a philosopher may continue to lose access to the required chopsticks, resulting in starvation.
6. Does preventing deadlock guarantee starvation-free execution?
No. Preventing deadlock only ensures that the system does not become permanently blocked through circular waiting. A philosopher may still be repeatedly bypassed while others continue eating. Guaranteeing starvation-free execution requires an additional fairness mechanism, such as bounded waiting or a fair FIFO policy for resource allocation.
