pow() in Python

Overview
In Python, the pow() function is used to calculate the nth power of a number (, where is a number and is its power). There are two types of pow() function, one is an inbuilt function, and the other one is imported from the math module.
Syntax of pow() in Python
Python has two types of pow() functions (inbuilt and imported from the math module).
Syntax of inbuilt pow() function
The inbuilt pow() function accepts three arguments (base, exponent, and modulus), out of which the modulus is an optional parameter.
Syntax of math.pow() function
The math.pow() function accepts two arguments (base and exponent)
Parameters of pow() in Python
Parameters of the inbuilt pow() function:
- base: Base is the number whose nth power is to be found. It can be an integer, floating point, or even a complex number.
- exponent: Exponent is the power to which the base is raised. It can be an integer, floating point, or even a complex number.
- modulus (optional): Modulus divides the result (base^exponent) and gives its remainder (result%modulus). It can be an integer only and is an optional parameter.
Parameters of the math.pow() function are the same as the inbuilt pow() except for the fact that it doesn't accept the 3rd argument (modulus). The parameters of the pow() function cannot be a complex number.
Return Values of pow() in Python
The return value of the inbuilt pow() function:
The inbuilt pow() function returns the value of the base to the power of the exponent (). The return value can be an integer, floating point, or complex number.
The return value of the math.pow() function:
The math.pow() function returns the value of base to the power of exponent (). The return value is always a floating point number.
Exceptions of pow() in Python
While the base and exponents of the pow() function can be negative, a floating point number, or even a complex number, there are some exceptions to the inbuilt pow() function when using the third argument (modulus)
ValueError: complex base with modulus in pow()
When we pass a complex number as the base while using the third argument (modulus), we get a "ValueError", which states that a complex number can't be used with a modulus.
TypeError: floating point number arguments with modulus in pow()
When we pass a floating point number as the base while using the third argument (modulus), we get a "TypeError", which states that floating-point arguments can't be used with a modulus as we can use modulus only with integers.
ValueError: negative exponent with modulus in pow()
When we pass a negative number as the exponent while using the third argument (modulus), we get a "ValueError", which states that a negative exponent can't be used with a modulus. This error is thrown because a negative exponent gives the result as a floating point number between 0 and 1; we already know that we cannot use a modulus with a floating point number.
ValueError: negative base with floating point exponent in math.pow()
When we pass a negative number as the base and a floating point number as the exponent to math.pow(), we get a "ValueError" as a result which states that we can't use a negative base with a floating point exponent.
OverflowError: Large values (greater than) returned with math.pow()
When we use math.pow(), the result can't be greater than , and if we try to return a number that big, we get an "OverflowError", which states that the calculated value overflows the range of math.pow() return value.
Example of pow() in Python
Source Code
Output
In the above example, we calculate the 3rd power of using the inbuilt pow() function. As a result, we get .
What is the pow() Function in Python?
The Python pow() function returns the power of the given numbers. There are two types of pow() function, one is inbuilt, and the other one is imported from the math module. The inbuilt pow() function is the same as using the ** operator.
Using the inbuilt pow() function, we can also find the modulus of the result using the optional third argument, which is not supported by the math pow() function. The modulus is useful in modular exponentiation (exponentiation performed over a modulus).
The pow() function is useful in complex calculations and helps write clean code (as implementing a power function can be trivial).

Differences between inbuilt pow() function and math.pow() function
| pow() | math.pow() |
|---|---|
| pow() is an inbuilt function. | math.pow() is imported from the math module. |
| It accepts an optional third argument (modulus). | It doesn't accept a third argument. |
| It accepts an integer, floating point, and complex numbers as base or exponent. | It accepts integer and floating point numbers. |
| It doesn't change its arguments. | It changes its arguments to floating point numbers. |
| The return value of pow() can be an integer, floating point, or even a complex number. | The return value of math.pow() is always a floating point number. |
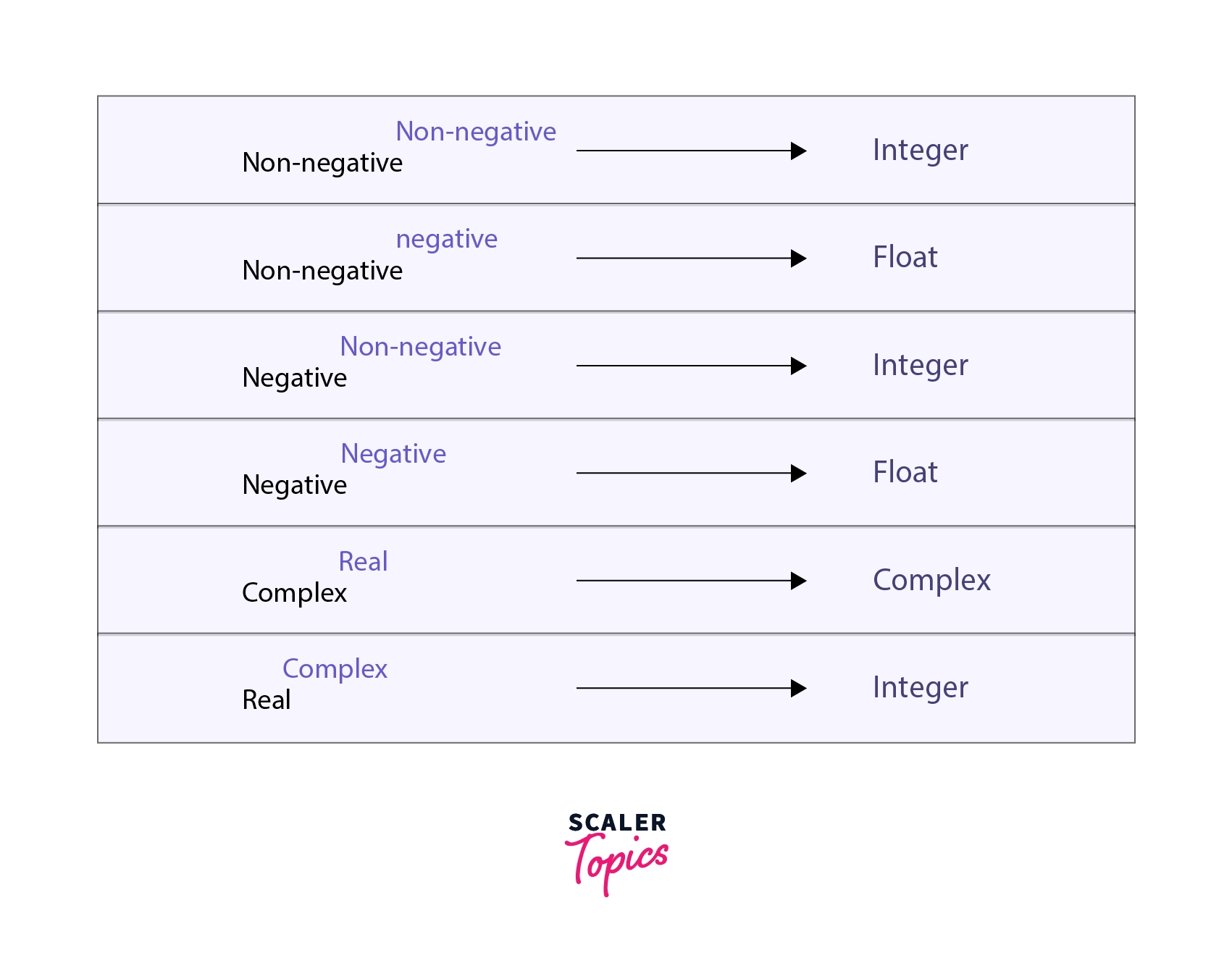
Implementation cases in pow()
The implementation cases of using the inbuilt pow() function
- Using a non-negative base with a non-negative exponent: Returns an integer
- Using a non-negative base with a negative exponent: Returns a floating point number
- Using a negative base with a non-negative exponent: Returns an integer
- Using a negative base with a negative exponent: Returns a floating point number
The implementation cases of using the math.pow() function
In math.pow() function, it doesn't matter if the base or exponent is negative or non-negative. The return value is always a floating point number.

More examples
Let's have a look at some more examples of the implementation of the pow() function for a better understanding:
Using the inbuilt pow() function with integers
Source Code:
Output:
In the above example, we are using the inbuilt pow() function with integers to calculate , and as a result, we get as the output.
Using the inbuilt pow() function with floating point numbers
Source Code:
Output:
In the above example, we are using the inbuilt pow() function with a floating point number to calculate , and as a result, we get as the output.
Using the inbuilt pow() function with complex numbers
Source Code:
Output:
In the above example, we are using the inbuilt pow() function with a complex number to calculate , and as a result we get in the output as , which further simplifies to .
Using the inbuilt pow() function with the third argument (modulus)
Source Code:
Output:
In the above example, we are using the inbuilt pow() function with the third argument (modulus) to calculate , and as a result we get in the output as and .
Using the math.pow() function
Source Code:
Output:
In the above example, we are using the math.pow() function to calculate , and as a result, we get as the output. The output is a floating point number because the math.pow() function converts its parameters (base and exponent) to floating point numbers.
Using a complex base with modulus
Source Code:
Error:
In the above example, we pass a complex number as the base while using the third argument (modulus), and as a result, we get a "ValueError", which states that we cannot use a complex base with the modulus.
Using floating point number arguments with modulus
Source Code:
Error:
The above example passes a floating point number as the base while using the third argument (modulus). As a result, we get a "TypeError" which states that we cannot use floating point number arguments with the modulus as we can use modulus only with integers.
Using negative exponent with modulus
Source Code:
Error:
In the above example, we pass a negative number as the exponent while using the third argument (modulus). As a result, we get a "ValueError", which states that we cannot use a negative exponent with the modulus.
This error is thrown because a negative exponent gives the result as a floating point number between and , and as we already know, we cannot use a modulus with a floating point number.
Using negative base with floating point exponent in math.pow()
Source Code:
Error:
ValueError: math domain error
res = math.pow(base, exponent)
Line 9 in <module> (Solution.py)
In the above example, we pass a negative integer as the base and a floating point number as the exponent to the math.pow() function. As a result, we get a "ValueError" which states that we cannot use a negative base with a floating point exponent.
Large values (greater than ) returned with math.pow()
Source Code:
Error:
In the above example, we calculate 1000^103 using the math.pow() function. As a result, we get a "OverflowError", which states that the calculated value overflows the range of math.pow() return value.
Conclusion
- The pow() function is used to find the nth power of a value.
- There are two types of pow() function: inbuilt and imported from the math module.
- The inbuilt pow() function accepts three arguments (base, exponent, and modulus), out of which the third argument (modulus) is optional.
- We can also find the nth power of complex numbers using the inbuilt pow() function.
- The math.pow() function accepts only two arguments (base and exponent).
