Array Data Structure
Overview
Array is defined as an ordered set of similar data items. All the data items of an array are stored in consecutive memory locations in RAM. The elements of an array are of same data type and each item can be accessed using the same name.
Takeaways
- Complexity of array
- Time complexity - O()
- Space complexity - O()
What is Array in Data Structure?
An array is a data structure containing items of similar data types. There, said it, the standard definition. How about, an array is simply a collection of elements having the same data type like cocktail names – Mojito, LIIT (choose a name, suit yourself according to taste). A list of cocktail names could be an array considering drink names are elements which are strings.
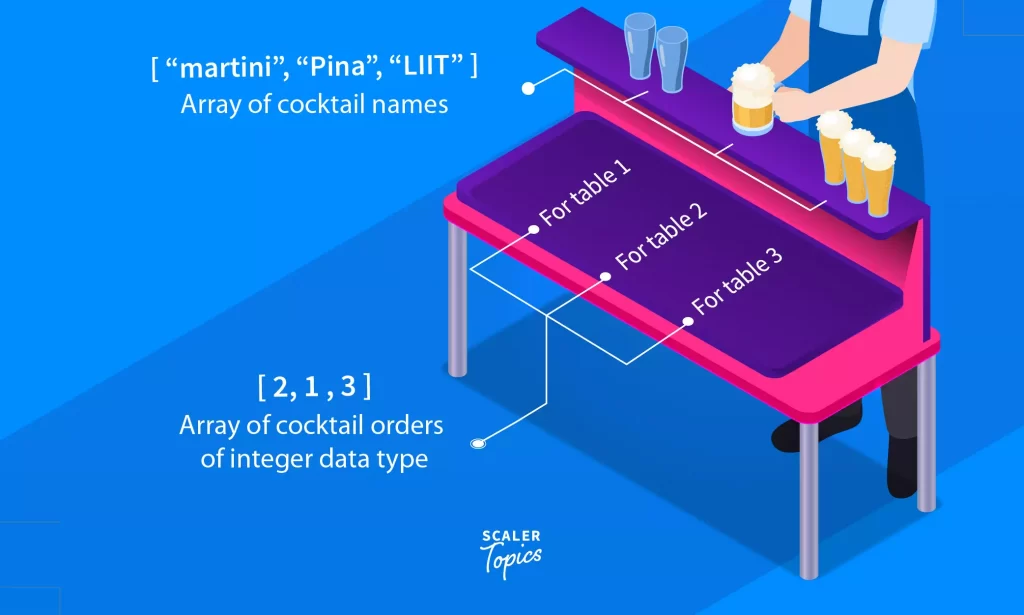
Another array could be a list of the number of cocktails which would be numbers, they can coexist separately as two different arrays of integer and string data type.
Representation of Array
Arrays can be represented in many ways.
Try to understand the code snippet given below:
This is how we declare an array in C like we declare variable.
Now in order to work around with the array you need to access the elements inside it, to access it we use:
Types of Array in Data Structure
We have multiple forms of arrays to ease the process of storing data further.
Array types depend on the number of dimensions an array can have. These are:
Single Dimensional Arrays
The arrays we discussed and declared in the previous section were 1D arrays because they stored elements linearly in continuous memory locations. Single dimension is used to store elements inside this array. They are denoted as Array_Name [ ].
Multi Dimensional Arrays
Arrays having more than one dimension are multiple dimensional arrays as the name suggests, they are further divided into two-dimensional (2D) arrays and three-dimensional (3D) arrays.
-
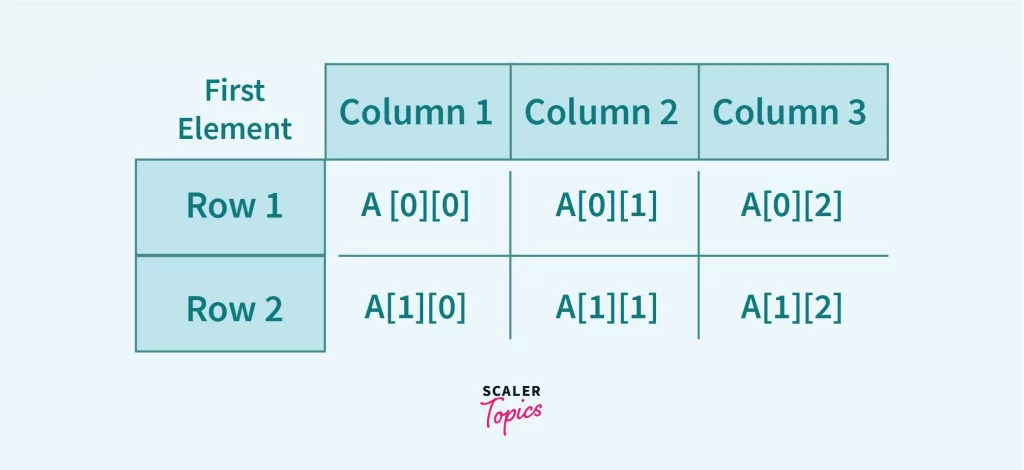
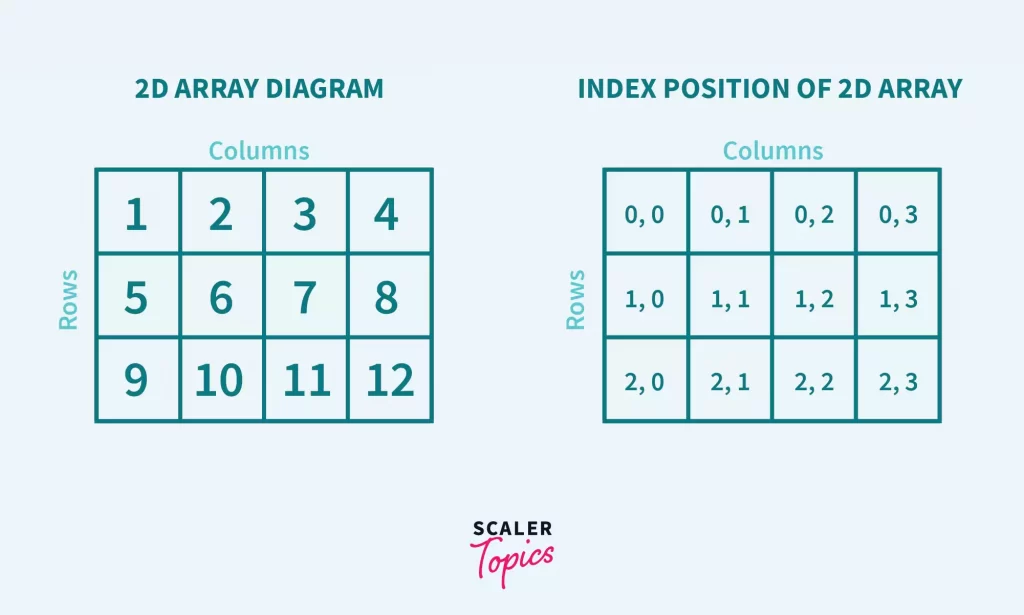
Two Dimensional Arrays– 2D arrays give us a tabular representation by storing elements in a form of rows(i) * columns(j), for instance an A[2][3] will have 2 rows and 3 columns allocating 6 elements. The array starts from A[0][0] which gives us the first element like shown in the image below.
-
Three Dimensional Arrays – A 3D array extends a 2D array by adding a dimension depth in this data structure, so this array has depth, rows and columns denoted as A[k][i][j] where k, i, j represents depth, rows and columns respectively. So evidently A[3][3][4] will have depth 3, 3 rows and 4 column:
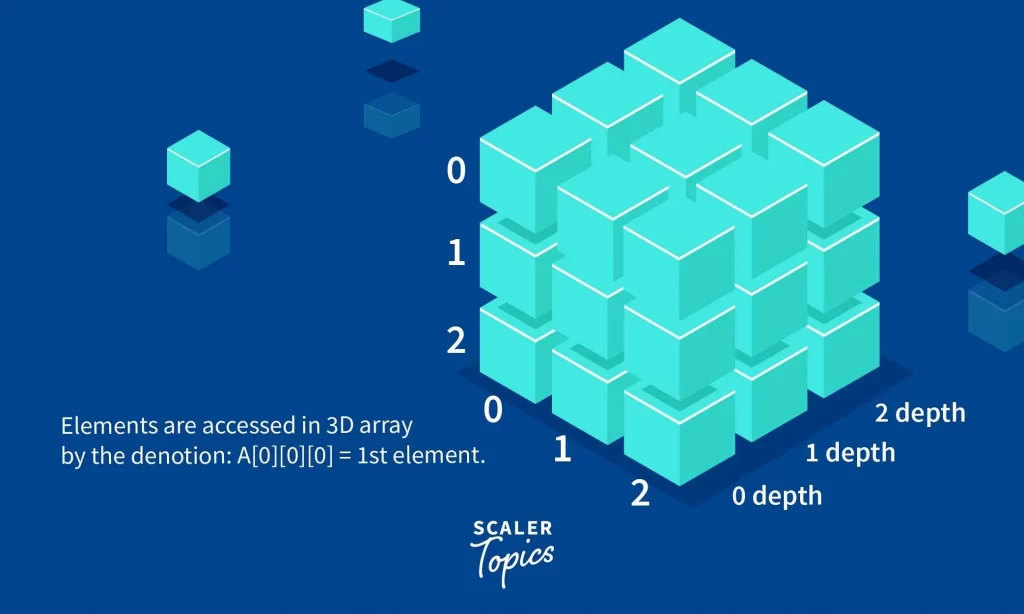
Elements are accessed in 3D array by the denotion: A[0][0][0] = 1st element.
Properties of an Array
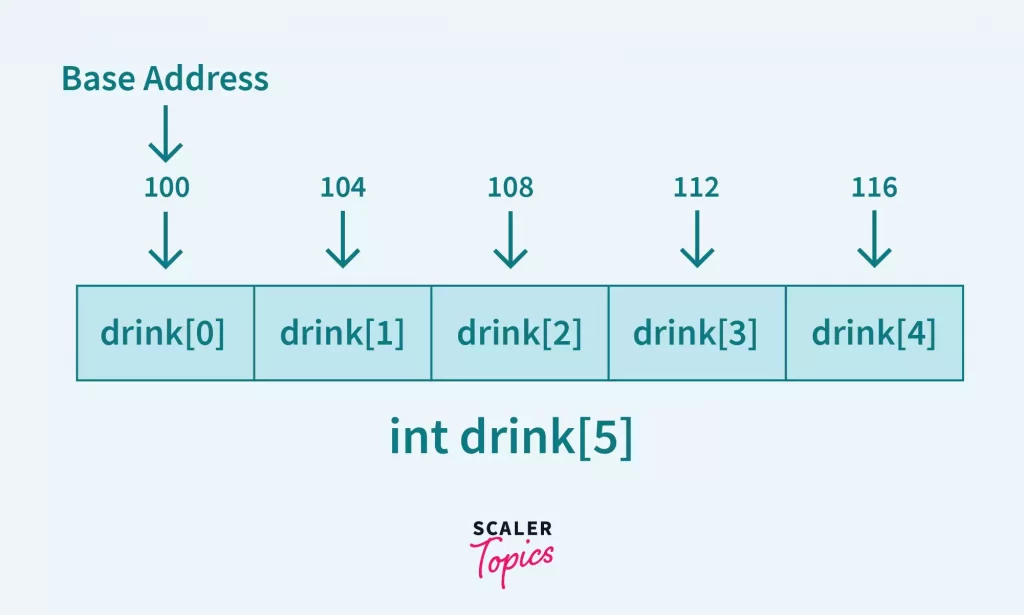
In an array, elements are stored in subsequent memory locations in primary memory. The array name is a pointer variable that represents the base address of an array.
In the below image, suppose the array’s base address i.e. the address of the first element of the array, is 100, and one int variable takes 4 bytes of memory(this is compiler dependent), so the next element exists on 104.
And the last element of the array exists on the 4th location since the array is of size 5 but the index in the memory starts from 0 so the index of the last element of an array will always be one short of array size (arraySize-1).
Basic Operations Performed with an Array
Operations in Array are like features of it, what an Array can do with the elements inside it is the operation of arrays. Arrays have 5 basic operations:
- Traverse: Traversing literally means travelling through an area, and in terms of a programming language it means running a loop in an array and performing the required operation.
- Insertion: Adding an element inside an array on the given position(index) in the array.
- Deletion: Removing any element from an array at a given position(index).
- Search: Searches an element of an array by the element index or the value.
- Update: Updates an element on a given position(index).
Note: In C, when an array is initialized with size then it assigns garbage values to its elements.
1. Traverse
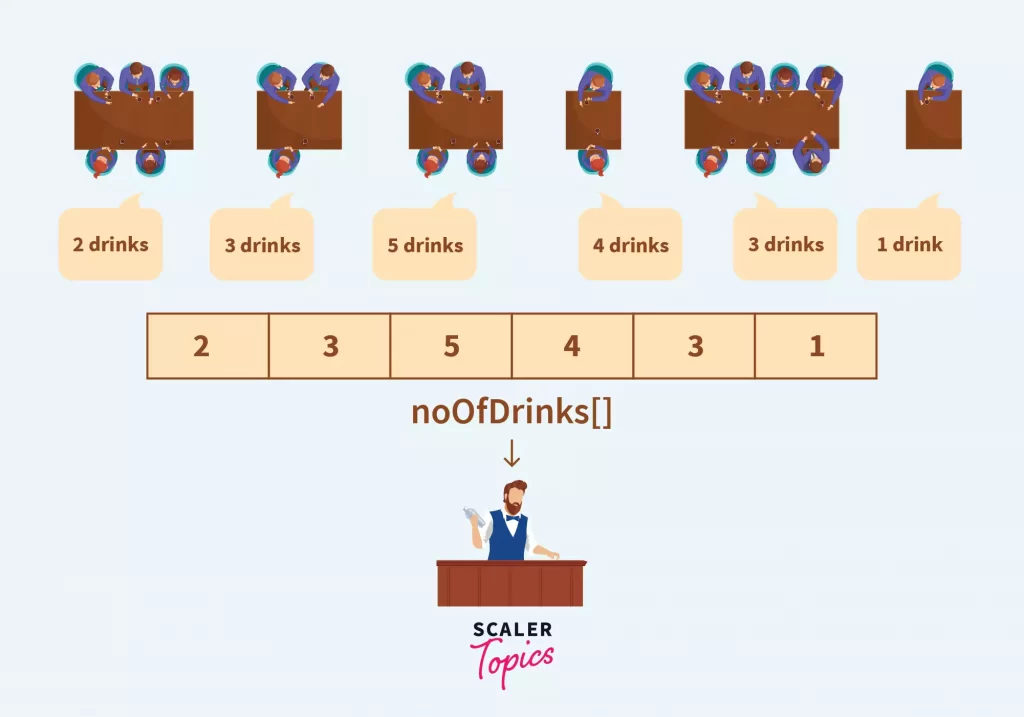
As we read above traversing means(literal) travelling through an area, here we refer to traversing as travelling through the elements which are present inside an array, could be an array of numbers (like number of cocktails ordered)
Now noOfDrinks represents the number of orders, suppose the first element represents the order for table number one i.e. table number 1 ordered 5 of our cocktails and so on.
For traversing in array of n number of elements, we’ll have to go through each element one by one so number of steps required to accomplish this will be n.
If there would have been just 1 element i.e. value of n equals one, we’ll require one step so the time complexity will be O(1).
Average or Worst Time Complexity : O(n)
Best Time Complexity : O(1)
2. Insertion
We can insert one or multiple elements in an array as per the requirement, of course, we can add an element at the beginning of the array or at the end of the array.
We can add an element anywhere in the array by giving the index(position) on which the element has to be added.
Suppose we had to lay an extra table so that makes six tables but we have 5 right now and due to the customer preference we have to arrange a table between 2nd table, 3rd table and to accommodate the table there we’ll have to move the 3rd table and all the remaining after 3rd.
Please don’t move forward until you imagine this picture and envision shifting the tables, read again, understand. Since we’ll have 6 tables, we have to expand our noOfDrinks array and insert an element(orders).
We have applied the same approach of shifting tables as you observed, shifting the elements after the 2 positions because we had to insert an element at the 2nd position:
- First step, we increment the size of the array in order to adjust the new element
- We adjust the value of loop counter ‘j’ so we can start the loop from the last element and then go towards the lower indexes.
- Then we put a while loop with condition, while j is greater than or equal to pos, the loop should execute.
- Observe the loop, the last element(5th) will be shifted to a new position (6th; which is now the last), similarly, 4th to 5th and so on, next we copied the new element to the required position and displayed it.
Time complexity of insertion would be the same as traversing. An element could be added at the starting index, last index or in the middle of the array. Adding an element in the middle or beginning of an array will have average to worst time complexity as every element after added element will shift its position by one but when the element is added in the at the end of the array only one step is required hence best time complexity.
- Average or Worst Time Complexity : O(n)
- Best Time Complexity : O(1)
3. Deletion
If any element can be inserted, it can be deleted too. Suppose the added table needs to be removed now since it was put on a special request but it’s congesting our prestigious bar. So now when we remove that added table we’ll have to bring back the orientation to the way it was, for that we’ll shift the tables back after the removed table i.e. 3rd table.
We have again gone to the previous orientation by copying the element on the 3rd position to the element on the 2nd position so the 2 position element will be deleted and then the element on the 4th position to 3rd and so on.
Deleting elements has the same scenario too. If the element has to be deleted from the beginning or anywhere from the middle of the array, remaining elements will have to shift their index so it will take n steps even if the index of element to be deleted is known, that means average or worst time complexity, however if the element deleted is the last element of the array, best time complexity.
- Average or Worst Time Complexity: O(n)
- Best Time Complexity: O(1)
4. Search
We can search any element in an array and display both its index(position) and the value.
Suppose we need to find the table number with the number of orders equal to 4, how do we find it though, check the order numbers one by one and determine the table number which has the same order number.
- Average or Worst Time Complexity: O(n)
- Best Time Complexity: O(1)
5. Update
The elements in the array can be updated as well, which means we can change the values of the elements inside an array.
- Time Complexity: O(1)
Advantages of Array
Let’s quickly go through some advantages arrays has:
- Easier to remember a group name than the individual names likewise it’s easier to remember an array name than remembering names of several variables.
- Traversing which we read above is a brilliant feature of arrays, it’s easy, incrementing the base address of the array lets us visit every element inside an array one after another.
- Any element of the array can be accessed by using the index(position) of the element in O(1) time complexity.
Dynamic Memory Allocation of the array
Let me jog your memory real quick, we discussed that declaration means allocating memory for the elements of an array of given size if any.
But that is static or compile-time memory allocation, which means the memory to an array element is allocated when your code is being compiled.
Now can we allocate memory at runtime, yes, we can use functions like malloc etc. of one of the several libraries? I just realized I typed it all over again, could’ve simply done copy-paste. What we need to understand primarily is, why this dynamic memory allocation. Whenever we are not sure about the exact size of an array until code is compiled by the compiler, the size of the array we declared could be less than required or even more than required. In such cases static memory allocation is not preferred.
Let us start with understanding what a library is, it is a collection of precompiled modules(stored in object format) available for use by other programs(consisting of code), like we wrote several above.
Library functions are built-in functions that are stored together in a location that is the library.
Every function has its unique ability, a very specific role just like our cocktail drinks, okay sorry, I won’t compare everything with our fabulous bar.
One more thing to use these functions we have to import it using header files just like we put at top of our every code snippet (#include ; stdio.h is one of the many header files ).
We have four library functions defined under <stdlib.h> header file which can be used to dynamically allocate memory:
- malloc() – The memory allocation method in C is used to dynamically allocate a single large block of memory with the specified size.
- calloc()- Contiguous allocation method in C is used to dynamically allocate the specified number of blocks of memory of the specified type.
- free() – method de-allocates the memory being used, dynamically. It is crucial as malloc() and calloc() do not deallocate memory on their own. It aims to reduce memory wastage.
- realloc()– method alters the memory allocation of already allocated memory. It is used in scenarios where the previously allocated memory is not insufficient, so realloc is used to dynamically re-allocate memory.
Note: This is a little heavy but concentrate, we will take up our beloved bar again.
Dynamic memory allocation is used more widely in complex problem scenarios than static because when you don’t even know the defined number of elements required, static memory allocation is possible but it could waste memory that is not really being used which is obviously not a good practice.
For example – we need to know the name and number of all the customers who will attend our bar’s upcoming anniversary so arrangements can be made accordingly as drinks are on the house, yes people getting drunk could be an example in education articles, we are in 2021. So since we sent 45 invites and our capacity to serve is 60 so we know the maximum size could be 60, we can declare an array with size 60 and insert their names as elements, easy, right? 15 turned up that day so 45 memory blocks were actually empty but allocated.
Imagine when this amount is in millions and only half is being used, so in scenarios when we don’t know the size, dynamic memory allocation is a better efficient practice than static memory allocation. Another use case could be when we need arrays that takes elements through user input.
Passing Array to the Function
Note: If you do not have much idea about functions in C, kindly check this article then come back here to understand this section:
We can pass arrays to the functions as arguments or parameters just like we pass variables.
Suppose we need to find the total number of drinks ordered in one go, we can easily design a function that gives us the sum of all the drinks but we have the number of drinks stored in an array right not in separate variables so the standard sum=a+b+c won’t work here. But since we know arrays can be passed to the functions in C, let us quickly see how:
We start by declaring the display function outside the main, we do this to let the compiler know that a function named display exists, we can write the function definition on top of the main then we won’t need the declaration. Then we call the function display passing noOfDrinks[] array as an argument. [] after array name is important as it indicates to the compiler that a one-dimensional array is being passed as a parameter or an argument. When a function is called, the program control is given to the called function and then function performs its task, when the last statement of the function is executed the control is given back to the program. After calling we define the function outside main.
Mapping 2D Array to 1D Array
2D arrays are actually there from the user point of view but the storage process of 2D array is the same as one-dimensional arrays we have been using this far. 2D arrays are created to give a tabular representation (in form of rows and columns), like a RDBMS.
The size of a 2D array is equal to the multiplication of the number of rows and columns of the array.
There are two major techniques of storing 2D arrays in memory, giving us two formulas to map a 2D array into 1D or finding the address of a random element in a 2D array.
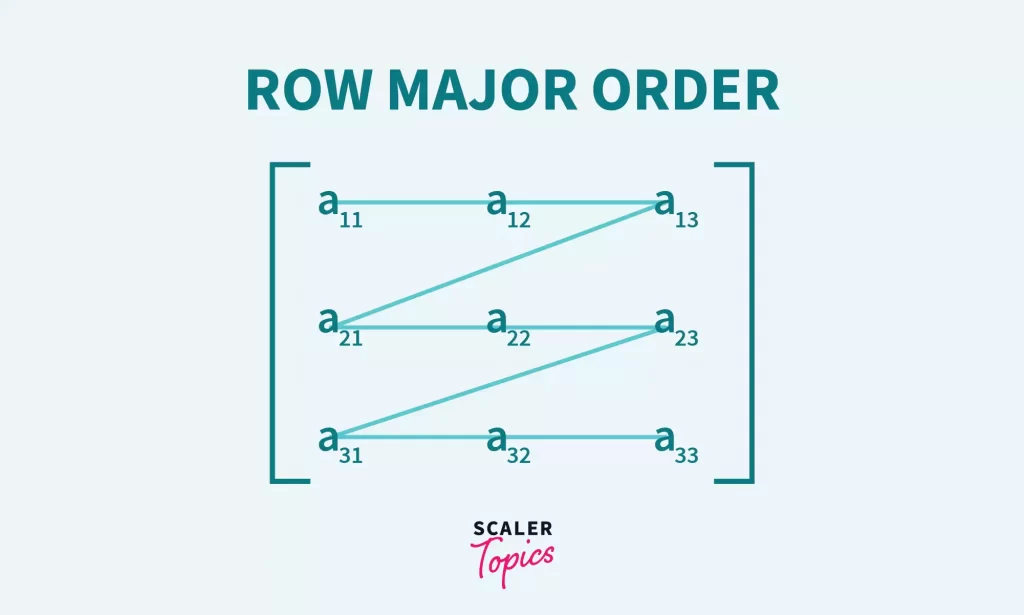
Row Major Order: All the rows of the array are stored in the memory continuously.
2D array Index 0,0 0,1 0,2 0,3 1,0 1,1 1,2 1,3 2,0 2,1 2,2 2,3
2D array elements 1 2 3 4 5 6 7 8 9 10 11 12
Starting with the first row getting stored in the memory, similarly storing second row so on till n rows.
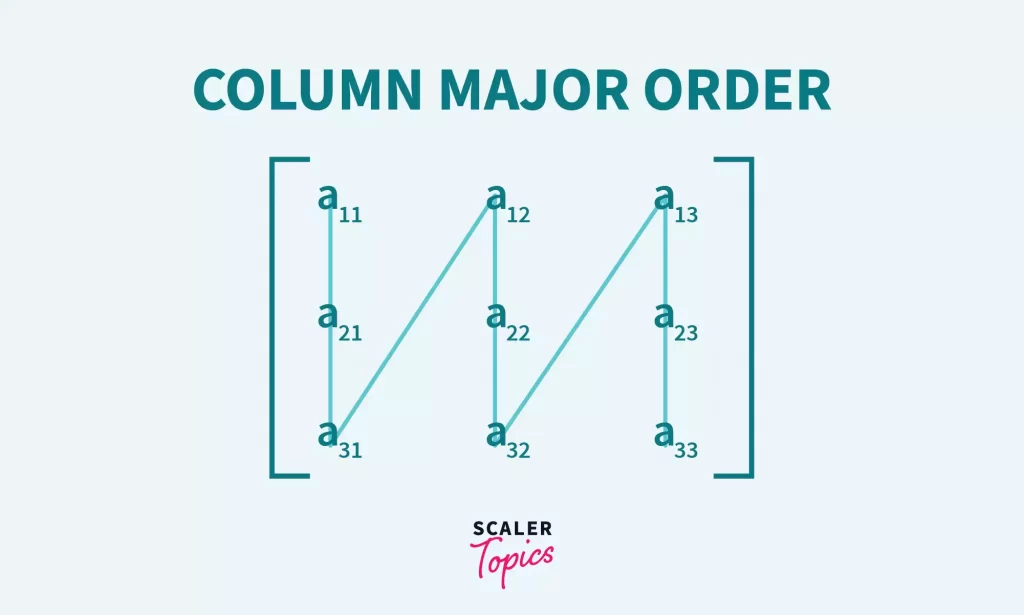
Column Major Order: All the columns of the array are stored in the memory continuously.
2D array Index
0,0 1,0 2,0 0,1 1,1 2,1 0,2 1,2 2,2 0,3 1,3 3,3
2D array elements
1 5 9 2 6 10 3 7 11 4 8 12
Starting with the first column getting stored in the memory, similarly storing the second row and so on till n columns.
Examples of mapping through each of the method
By Row Major Order:
If an array is of the form a[p][q] where p represents number of rows and q represents number of columns, the address of an element a[i][j] of this array stored in row major order is calculated as:
Address(a[i][j]) = BaseAddress + (i*q + j)*Size
By Column Major Order:
If an array is of the form a[p][q] where p represents number of rows and q represents number of columns, the address of an element a[i][j] of this array stored in column-major order is calculated as:
Address(a[i][j]) = BaseAddress + (j*p + i)*Size
Boost Your Tech Profile! Join Our DSA Courses for Advanced Algorithmic Mastery. Enroll Now to Stand Out in the Coding Landscape!
Conclusion
All in all, after our discussion we can come to an undisputed conclusion that arrays offer a simple way out in scenarios where elements of the same data type have to be used by grouping elements and then accessing them through indexing, also enabling us to perform different operations. It is definitely a better way than declaring and calling variables again and again and if you disagree on that, do contact us.
Note: Do you remember us discussing that elements in an array are stored in subsequent memory blocks of information or data so they can be also accessed through pointers.

